Июнь 2018, 10-й тур
Этот тур конкурса уже прошел. Чтобы посмотреть задания, нажмите на название раздела.
Если вы только недавно присоединились к конкурсу и хотите порешать старые задания - милости просим.
Задания отправлять можно, мы их проверим и пришлем ответ.
Баллы за отправленные позже срока задания не учитываются.
Расшифруйте ребус АХ + ОХ = ОДА. (Найдите все ответы и докажите, что других нет. Одинаковыми буквами обозначены одинаковые цифры, разными – разные, и ни одно число не начинается с ноля.)

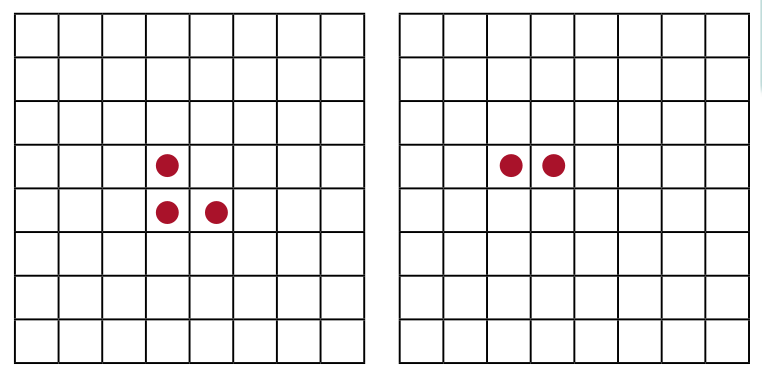
На клетчатой доске стоят три фишки (как показано на левом рисунке). Одним ходом можно одновременно передвинуть одну фишку вверх (на одну клетку), одну фишку влево (на одну клетку) и одну фишку по диагонали вправо-вниз (на одну клетку). После нескольких таких ходов две фишки встали, как показано на правом рисунке. Где могла оказаться третья фишка?

Олег устраивает вечеринки исключительно по пятницам 13-го. Мог ли он остаться без вечеринок в каком-нибудь году? А какое наибольшее число вечеринок может быть у Олега за год?

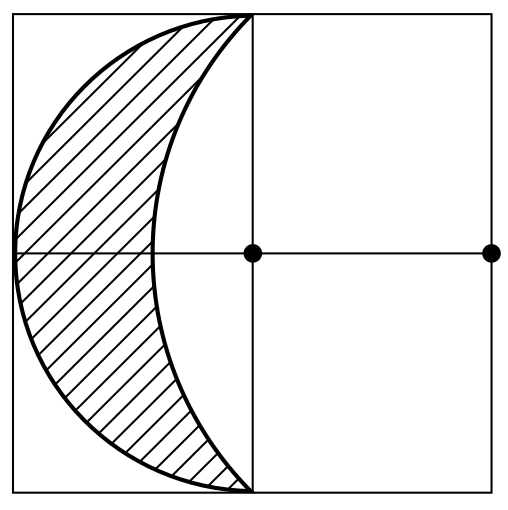
На клетчатой бумаге провели две окружности с центрами в отмеченных точках. Их дуги ограничивают заштрихованную фигуру. Найдите её площадь, если площадь одной клетки равна 1.

У эксперта есть 8 золотых пластин, промаркированных 10 г, 20 г, 30 г, 40 г, 50 г, 60 г, 70 г и 80 г, а также слабочувствительные двухчашечные весы без гирь. Более тяжёлая чашка этих весов перевесит, если разность весов на чашках больше 10 г, иначе весы останутся в равновесии. Эксперт знает, что вес ровно одной из пластин меньше заявленного. Как ему определить эту пластину на таких весах за 3 взвешивания?
