• Март 2018, 7-й тур

    Этот тур конкурса уже прошел. Чтобы посмотреть задания, нажмите на название раздела.

    Если вы только недавно присоединились к конкурсу и хотите порешать старые задания - милости просим.
    Задания отправлять можно, мы их проверим и пришлем ответ.
    Баллы за отправленные позже срока задания не учитываются.


    • Задача 31 Задание

      31. (Егор Бакаев) Разрежьте фигурку на рисунке на 5 одинаковых частей.


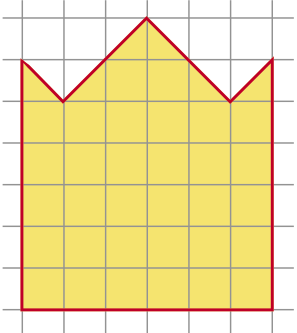
      (Дополнение: клетки квадратные. Скорее всего, у вас они и так квадратные, но на некоторых мониторах они могут отображаться немного сплюснутыми).


    • Задача 32 Задание

      32. (Григорий Гальперин) Количество цифр в числе N в 2018 раз меньше, чем само число N. Чему может равняться N? 
      (Найдите все возможные варианты и докажите, что других нет.)



    • Задача 33 Задание

      33. (Сергей Костин) Два игрока по очереди нанизывают красные, синие и зелёные кольца на 33 стержня. У каждого игрока неограниченное количество колец каждого типа. За ход игрок нанизывает какое-либо кольцо на какой-то стержень. Запрещается помещать красное кольцо непосредственно на синее, а синее – непосредственно на зелёное. Также на стержне не может быть более одного кольца каждого цвета. Проигрывает тот, кто не может сделать ход. Кто из игроков может всегда выигрывать, как бы ни играл его соперник?


    • Задача 34 Задание

      34. (Гриша Никитин) 
      а) Петя пишет в каждой клетке доски 100x100 буквы А или Б так, чтобы всего на доске их было поровну. Вася передвигает по этой доске фишку, сдвигая её всё время только в соседнюю клетку и каждый раз записывая, на какой букве она стоит. Всегда ли Вася может так поставить фишку и так обойти ею все клетки ровно по одному разу, чтобы полученная  последовательность букв одинаково читалась слева направо и справа налево?

      б) То же самое для доски 101x101, букв А на одну больше, чем букв Б.

    • Задача 35 Задание

      35. (Игорь Акулич)
       – Поделил я как-то одно натуральное число на другое с остатком, – рассказывал Петя Коле. – Когда же я поделил квадрат первого числа на второе, остаток оказался вдвое больше, чем был при первом делении. А когда я поделил куб первого числа на второе, остаток стал уже втрое больше.
      – Ну, это ты заливаешь, такого не может быть! – воскликнул Коля. – Вот со мной действительно была похожая история. Я тоже поделил одно натуральное число на другое с остатком. И когда я поделил куб первого числа на второе, остаток оказался вдвое больше первоначального, а когда поделил квадрат первого числа на второе, остаток стал втрое больше.
      – Теперь уже ты сочиняешь! – заявил Петя.

      Кто мог быть прав в каждом случае?